Analisi econometrica e statistica di una serie storica con Python

Utilizziamo strumenti di analisi statistica e econometrica per l’analisi di una serie storica

Aiutiamoci con Python per la parte di analisi dei dati e previsioni di una ipotetica time series

In quest’articolo guida realizzeremo un’analisi econometrica e statistica di una serie storica sfruttando le potenzialità di Python.

L’intero codice usato in quest’articolo è open source.

Oltre agli snippet già inseriti nel testo dell’articolo e disponibili su GitHub Gist, è possibile scaricare l’intero file sorgente (Jupyter Notebook interattivo).

Le indicazioni e link sono fornite di seguito nell’articolo.

Analisi econometrica e statistica di una serie storica con Python

Introduzione

Una serie storica (in inglese time series) è una sequenza ordinata di osservazioni di una variabile nel tempo, raccolte a intervalli regolari. Le serie storiche costituiscono uno strumento fondamentale nell’analisi dei dati temporali.

Le serie storiche si distinguono per alcune caratteristiche peculiari che le rendono diverse dalle altre strutture dati:

Dipendenza temporale: i valori successivi della serie sono generalmente correlati tra loro. A differenza dei campioni indipendenti, in una serie storica l’ordine delle osservazioni ha importanza.
Tendenza (trend): componente deterministica che rappresenta la variazione a lungo termine della serie.
Stagionalità: fluttuazioni regolari e prevedibili che si ripetono in un ciclo fisso (giornaliero, settimanale, annuale).
Ciclicità: variazioni non regolari, associate a cicli economici o fenomeni naturali di lungo periodo.
Rumore (noise): componente aleatoria, non prevedibile, residua dopo aver rimosso tendenza e stagionalità.

Obiettivo dell’analisi

L’obiettivo è duplice: da un lato, esplorare le caratteristiche statistiche e temporali della variabile attraverso tecniche descrittive e visualizzazioni avanzate; dall’altro, costruire un modello econometrico in grado di cogliere le principali componenti dinamiche della serie storica e produrre previsioni a breve termine.

L’analisi si fonda su una pipeline in linguaggio Python, impiegando strumenti propri della statistica classica e della modellazione time series, con particolare riferimento ai modelli SARIMA (Seasonal Autoregressive Integrated Moving Average, o Seasonal ARIMA).

Tale approccio consente di integrare la componente stagionale, presente nei dati orari e giornalieri di diverse serie storiche, in una struttura autoregressiva differenziata a media mobile.

L’articolo si articola in una fase preliminare di esplorazione e trasformazione dei dati, seguita da una sezione di modellazione statistica e da un commento conclusivo sui risultati ottenuti e sulle possibili estensioni.

Descrizione: individuare tendenze, stagionalità, strutture autoregressive.
Forecasting: prevedere i valori futuri della variabile.
Modeling: stimare modelli generativi (es. ARIMA, GARCH) per comprendere le dinamiche sottostanti.
Controllo e rilevamento di anomalie: individuare cambiamenti strutturali o eventi fuori norma.

Sommario

Questo tutorial per l’analisi statistica e descrittiva di serie storiche mediante Python si pone i seguenti obiettivi:

Gestire il caricamento e la preparazione dei dati.
1. Parsing del file Excel in Python con pandas.
2. Pulizia dei dati (gestione dei valori nulli, normalizzazione timestamp, ecc.).
Effettuare l’analisi descrittiva del dataset
1. Statistiche riassuntive (media, mediana, varianza, ecc.).
2. Grafici: serie temporale, istogramma, boxplot per ora/giorno/settimana.
3. Analisi di stagionalità (es. differenze giorno/notte, feriali/festivi).
Procedere con alcune analisi econometriche
1. Test di stazionarietà (Dickey-Fuller).
2. Differenziazione se necessario.
3. Autocorrelazione (ACF/PACF).
4. Modello ARIMA o SARIMA per modellare la serie.
5. Eventuale previsione su periodo successivo.
Fornire alcuni esempi di data visualization
1. Time series grafica.
2. Boxplot.
3. Heatmap oraria (giorni vs ore).
Trarre alcune conclusioni con piglio critico
1. Riassunto dei risultati principali.
2. Interpretazione economica delle dinamiche valoriali.

Alcune premesse

I valori forniti nella serie storica sono del tutto fittizi. La serie storica utilizzata nell’articolo è stata creata per ottenere un andamento basato su tendenze (trend), ma senza tenere conto della realisticità dei valori assoluti esposti.
L’articolo è puramente divulgativo. Le previsioni fornite sono volutamente semplificate e non adatte a reali applicazioni.
Il codice creato è pensato esclusivamente per un uso didattico e non creato per un uso in produzione.
Trattare esaustivamente e scientificamente analisi di questo tipo richiederebbe una mole di spazio, tempo e risorse fuori scopo per le finalità di quest’articolo. Si intende ragionevole aver apportato semplificazioni in sede di analisi (vedere la sezione dedicata a seguire nell’articolo) e aver trattato in via semplificata dal punto di vista teorico alcuni passaggi sulla congruità del modello adottato.
In alcune sezioni l’output del codice è stato semplificato per rendere la lettura più agevole e scorrevole; viene fornita comunque la sorgente puntuale per riprodurlo localmente.

Bibliografia

Numerosi sono gli articoli e i paper che trattano l’utilizzo di modelli autoregressivi con stagionalità per le serie storiche.

In particolare, sono stati consultati:

Descrizione dei dati

L’analisi si basa su una serie storica oraria ipoteticamente a copertura di un anno solare (gennaio – dicembre), costituita quindi da 8.784 osservazioni, pari al numero di ore effettive in un anno bisestile. I dati sono organizzati in formato tabellare, con tre colonne principali: la data, l’ora (espressa in formato 1–24) e il valore orario.

Nel processo di importazione e preprocessing, particolare attenzione è stata dedicata alla costruzione di un indice temporale coerente. La combinazione della colonna “Time” e “Value” è stata utilizzata per generare un oggetto datetime completo a risoluzione oraria. È stata inoltre effettuata una conversione dell’ora dal formato 1–24 al formato 0–23, coerente con le convenzioni dei principali strumenti di analisi temporale in ambiente Python.

Durante la normalizzazione del calendario orario, è emersa la necessità di gestire le ambiguità dovute al cambio tra ora solare e ora legale. Tali transizioni possono generare duplicati o buchi nella sequenza temporale, fenomeno che è stato trattato attraverso una localizzazione temporale nel fuso Europe/Rome e una successiva conversione neutra (tz_convert(None)), con eventuale eliminazione delle osservazioni ambigue.

La variabile di interesse, ovvero il valore orario, è stata convertita in formato numerico a partire dalla rappresentazione testuale contenente la virgola come separatore decimale. Sono stati inoltre eseguiti controlli di consistenza e rimozione di eventuali valori anomali o duplicati.

A valle di queste operazioni, si dispone di una serie temporale regolare, pronta per l’analisi.

Analisi descrittiva della time series

L’esame preliminare della serie storica consente di ottenere informazioni significative sulla distribuzione, la variabilità e i pattern ricorrenti del valore orario nel corso del periodo considerato.

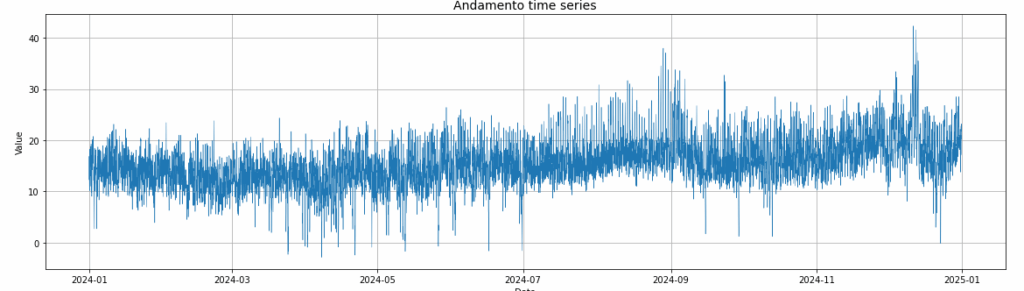
In primo luogo, la distribuzione dei valori di prezzo presenta una forma asimmetrica, con presenza di code a destra (right skewness) e occasionali outlier corrispondenti a picchi.

La statistica descrittiva elementare evidenzia una media su base annua pari a 15, con una deviazione standard prossima a 4.71 (coefficiente di variazione (CV) pari a ~ 31%).

Il range osservato si estende da un minimo inferiore a -2.86 a un massimo superiore a 40, valori che in un contesto reale possono riflettere le dinamiche estreme registrate in alcune fasce orarie, soprattutto nei periodi di stress stagionale o in corrispondenza di festività.

L’analisi della struttura infra giornaliera rivela una marcata stagionalità oraria.

I boxplot per ora del giorno mettono in luce una concentrazione dei valori più elevati nelle fasce diurne, in particolare tra le 8:00 e le 20:00, ipotizzando valori più volatili durante le ore di attività giornaliera (es. scambi sui mercati, produzione industriale, utilizzo di strumenti, etc.).

Elementi di data visualization

Un ulteriore elemento di interesse riguarda la variabilità settimanale.

Il confronto tra i boxplot per giorno della settimana mostra una riduzione della mediana e della dispersione nei fine settimana, in particolare la domenica, mantenendo una coerenza fattuale con ipotetiche osservazioni legate all’attività effettiva di un settore industriale, finanziario, o simili.

Tali osservazioni sono ulteriormente rafforzate dal comportamento della media giornaliera, che, tracciata lungo l’intero arco dell’anno, presenta un andamento oscillante ma con segnali di ciclicità settimanali e una tendenza generale sommariamente stabile nel medio periodo.

A completamento dell’analisi esplorativa, è stata realizzata una mappa di calore (heatmap) con rappresentazione bidimensionale dei valori medi orari per ciascun giorno dell’anno.

La visualizzazione, ottenuta mediante una riorganizzazione dei dati in una matrice giorno-ora, consente di individuare pattern stagionali ricorrenti e anomalie locali, offrendo una panoramica sintetica ma informativa su scala annuale.

Tali risultati descrittivi costituiscono la base conoscitiva necessaria per la successiva fase di modellazione econometrica.

Analisi statistica di una serie storica con Python – il codice

Di seguito il codice per questa prima parte di analisi:

Output:

                          Date  Time  Value
Timestamp                                  
2024-01-01 00:00:00 2024-01-01     0  12.30
2024-01-01 01:00:00 2024-01-01     1  16.86
2024-01-01 02:00:00 2024-01-01     2  12.29
2024-01-01 03:00:00 2024-01-01     3  12.24
2024-01-01 04:00:00 2024-01-01     4  10.14
count    8783.000000
mean       15.511005
std         4.711489
min        -2.860000
25%        12.600000
50%        15.270000
75%        18.140000
max        42.300000
Name: Value, dtype: float64

Qui la parte grafica relativa alla distribuzione dei valori. La distribuzione mostra una chiara deviazione dalla normalità, sia per l’asimmetria che per la presenza di code pesanti (fat tails).

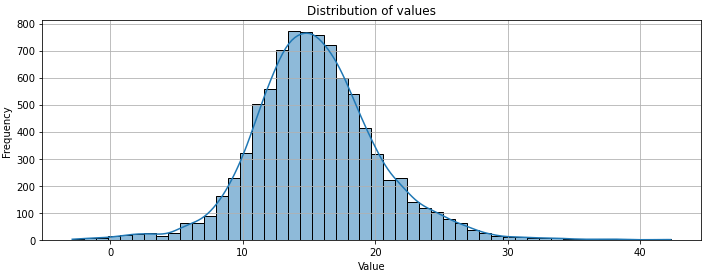Questo conferma l’adeguatezza di:

Modelli robusti (es. SARIMA, anziché modelli gaussiani),
Tecniche che non assumono simmetria o varianza costante.

Boxplot

Una ulteriore rappresentazione grafica mediante boxplot orario permette di apprezzare in modo più immediato il trend dei valori per singola ora (aggregata) del giorno.

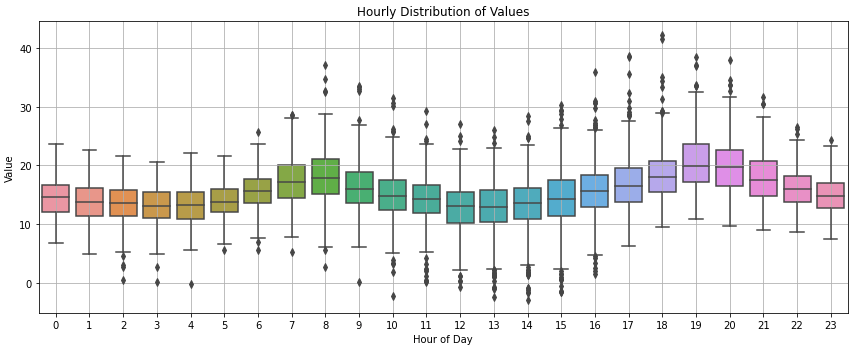
Un esempio di data visualization – Heatmap Oraria

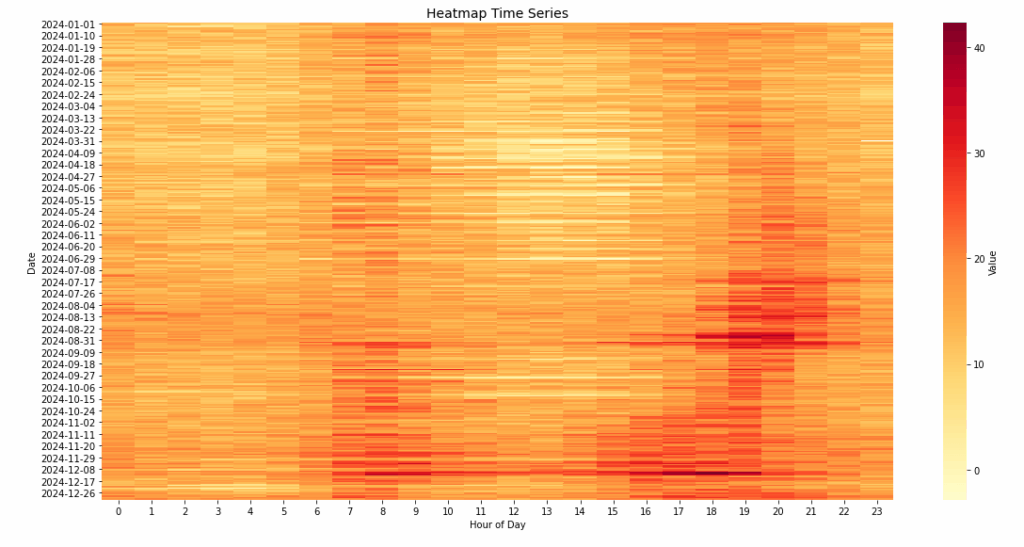
Nell’ambito delle serie temporali ad alta frequenza, la rappresentazione bidimensionale tramite mappa di calore (heatmap) costituisce uno strumento particolarmente efficace per l’analisi esplorativa di pattern ricorrenti e anomalie locali.

Applicata ai dati orari della serie temporale ipotizzata, la heatmap consente di evidenziare con immediatezza la struttura stagionale infra-giornaliera e le sue variazioni nel tempo.

La costruzione della visualizzazione si basa sulla riorganizzazione dei dati in una matrice in cui ciascuna riga corrisponde a una giornata dell’anno, mentre ciascuna colonna rappresenta una specifica ora del giorno (da 0 a 23).

I valori riportati nella griglia sono i valori orari, codificati cromaticamente attraverso una scala continua di intensità.

Tale rappresentazione consente di leggere verticalmente la dinamica quotidiana dei valori osservati e orizzontalmente le variazioni sistematiche per ciascuna fascia oraria lungo l’anno.

Dall’analisi visiva emergono chiaramente le fasce orarie a maggiore intensità coerenti con le ipotesi stabilite, localizzate tipicamente tra le 8:00 e le 20:00, coerenti con i picchi di attività di una ipotetica attività attiva nei giorni feriali e nel periodo diurno. Al contrario, le ore notturne mostrano una colorazione più tenue, indicativa di livelli di valori inferiori e più stabili.

Le giornate festive e i fine settimana si distinguono per una minore escursione cromatica, riflettendo la compressione della variabilità in condizioni di ridotta attività produttiva.

Sono inoltre osservabili alcuni episodi puntuali di pricing anomalo, che si manifestano come macchie cromaticamente intense, isolate rispetto alla struttura ricorrente.

Tali eventi possono essere attribuiti a fattori esogeni quali condizioni metereologiche estreme, indisponibilità infrastrutturale o dinamiche di mercato o produzione straordinarie.

La heatmap oraria, pur essendo una rappresentazione sintetica, offre una panoramica esaustiva e ad alta densità informativa sull’evoluzione dei valori nel tempo e nello spazio orario.

In particolare, essa risulta utile per il confronto visivo tra periodi, l’identificazione di regolarità settimanali e l’individuazione di deviazioni significative rispetto al comportamento atteso.

Heatmap dei valori orari – il codice

Analisi econometrica di una time series

L’analisi econometrica delle serie temporali ha come obiettivo la modellazione delle dipendenze dinamiche all’interno dei dati, con lo scopo sia di comprendere le componenti strutturali della serie, sia di effettuare previsioni a breve termine.

Nel contesto della serie storica ipotizzata, l’elevata frequenza temporale, la presenza di stagionalità multiple e l’esistenza di shock esogeni rendono necessaria l’adozione di un modello in grado di gestire congiuntamente le componenti autoregressive, differenziate, e stagionali.

A tal fine, si è fatto ricorso alla classe dei modelli SARIMA (Seasonal AutoRegressive Integrated Moving Average).

Motivazioni per la scelta del modello SARIMA

I modelli SARIMA rappresentano un’estensione naturale della famiglia ARIMA, introdotta da Box e Jenkins, che consente di includere componenti stagionali mediante la specificazione di termini addizionali a periodicità fissa.

La struttura generale del modello è indicata dalla notazione (p, d, q) (P, D, Q)s, dove:

p,d,q rappresentano rispettivamente l’ordine autoregressivo, il grado di differenziazione e l’ordine della media mobile per la componente non stagionale;
P,D,Q rappresentano gli stessi parametri per la componente stagionale;
s è la periodicità stagionale, espressa in numero di osservazioni.

L’impiego del SARIMA si giustifica nel caso in esame per la presenza evidente di una stagionalità settimanale e infra-giornaliera nei dati orari osservati.

Le analisi descrittive precedenti hanno mostrato pattern ricorrenti nei giorni della settimana e nelle ore della giornata, rendendo indispensabile l’utilizzo di un modello in grado di catturare tali regolarità.

Complessità computazionale e necessità di semplificazione

L’applicazione diretta di un modello SARIMA alla serie oraria completa annuale, con oltre 8.700 osservazioni e stagionalità infra-settimanale (s=168), comporta una significativa complessità computazionale. In particolare, la stima dei parametri su una serie di tale lunghezza, combinata con la presenza di differenziazione stagionale, può risultare proibitiva in termini di tempo di calcolo e stabilità numerica, soprattutto in ambiente monothreaded.

La memoria richiesta per il mero calcolo supera gli 8GB allocati stabilmente per circa 9 ore di run, su una macchina con dotazione standard da ufficio.

Per rendere l’analisi praticabile e mantenere al contempo un discreto grado di rappresentatività della dinamica di fondo, si è deciso di ricorrere a una versione semplificata della serie, mediante due trasformazioni:

Aggregazione giornaliera: si è passati da una granularità oraria a una media giornaliera, ottenendo una serie di 366 punti (anno bisestile), che conserva la struttura stagionale settimanale e riduce drasticamente la dimensionalità del problema.
Selezione temporale: è stato analizzato un sottoinsieme della serie (ad esempio, il primo trimestre dell’anno), in modo da ridurre ulteriormente la complessità e agevolare una stima preliminare dei parametri.

Queste scelte, seppur semplificative, non compromettono la validità dell’analisi, in quanto la componente settimanale resta osservabile nella serie aggregata e il comportamento dinamico rimane rappresentativo – pur all’interno di un contesto certamente didattico.

Verifica della stazionarietà

Prima della stima del modello, è necessario accertarsi che la serie sia stazionaria, ovvero che le sue proprietà statistiche (media, varianza, autocorrelazione) non varino nel tempo.

A tal fine è stato impiegato il test di Dickey-Fuller aumentato (ADF), il quale verifica l’ipotesi nulla di non stazionarietà.

Nel caso delle osservazioni su base giornaliera, il test ADF applicato alla serie grezza ha evidenziato un valore di p-value superiore alla soglia di significatività (tipicamente 0.05), indicando la necessità di differenziare la serie.

La differenziazione al primo ordine ha portato a una serie stazionaria, confermata da una successiva applicazione del test ADF, con p-value inferiore al 5%.

Stima del modello SARIMA

Sulla base della serie differenziata e aggregata, è stato stimato un modello SARIMA con struttura (1, 1, 1) (1, 1, 1) 7, che incorpora una stagionalità settimanale (7 giorni).

La scelta dei parametri è stata guidata dalla valutazione dei grafici di autocorrelazione (ACF) e autocorrelazione parziale (PACF), oltre che da criteri informativi come l’Akaike Information Criterion (AIC). Tale metrica è calcolata mediante la funzione .fit().

La stima del modello ha prodotto coefficienti significativi e una struttura dei residui coerente con l’ipotesi di rumore bianco.

I grafici diagnostici hanno confermato l’assenza di autocorrelazione residua e una distribuzione approssimativamente normale degli errori, indicando un buon adattamento del modello alla serie.

Previsione e valutazione

Il modello stimato è stato utilizzato per produrre una previsione su un orizzonte di 14 giorni.

Il forecast include intervalli di confidenza al 95%, calcolati sulla base dell’incertezza stimata dei parametri.

I risultati mostrano una continuità coerente con l’andamento osservato e mantengono le oscillazioni stagionali settimanali, evidenziando la capacità del modello di catturare correttamente la struttura ciclica della time series ipotizzata.

La valutazione del modello può essere ulteriormente affinata mediante l’utilizzo di misure di errore previsivo (MAE, RMSE) su un set di validazione, ma tale approfondimento esula dagli obiettivi primari di questa analisi.

Analisi econometrica di una time series con Python – il codice

Segue il codice per questa parte di analisi focalizzata sull’analisi econometrica.

A seguire i principali output:

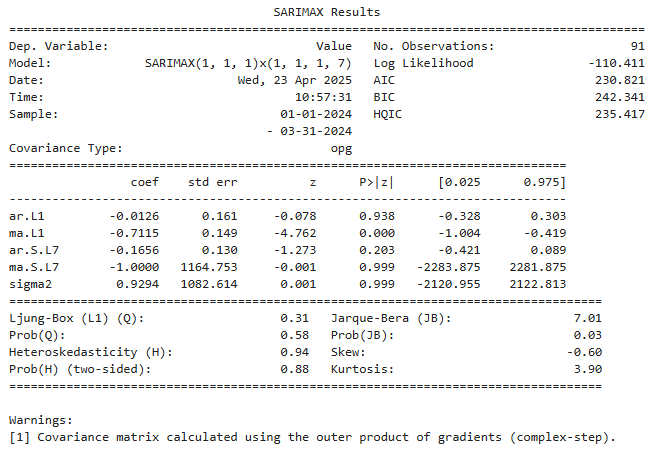
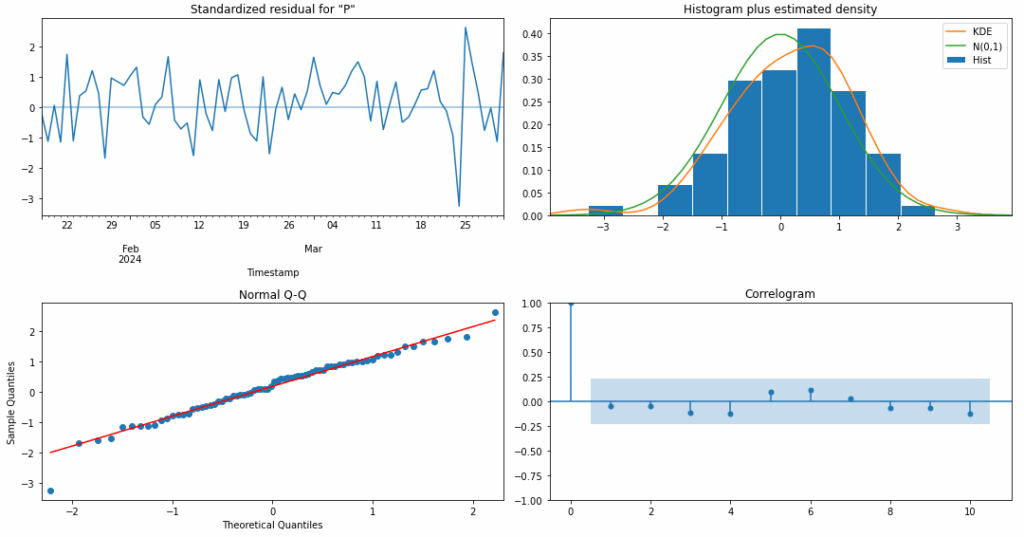
Interpretazione sintetica dell’output ottenuto

Una fase essenziale nella validazione di un modello SARIMA consiste nell’analisi dei residui standardizzati, al fine di verificarne l’aderenza all’ipotesi di rumore bianco, ovvero una sequenza priva di autocorrelazione, a media zero e varianza costante. I grafici diagnostici riportati permettono di valutare simultaneamente la struttura seriale, la distribuzione e la normalità dei residui.

Nel pannello superiore sinistro, la serie dei residui non mostra pattern sistematici nel tempo, suggerendo l’assenza di strutture autoregressive residue.

Il pannello superiore destro confronta l’istogramma dei residui con la densità normale standard e una stima non parametrica (KDE): la distribuzione appare simmetrica e ben centrata attorno allo zero, con una leggera curtosi positiva.

Il grafico Q-Q (quantile-quantile), in basso a sinistra, evidenzia un buon allineamento tra i quantili empirici e quelli teorici di una distribuzione normale, confermando la plausibilità dell’ipotesi di normalità.

Infine, l’ACF dei residui (correlogramma in basso a destra) mostra valori contenuti entro le bande di confidenza, senza evidenti autocorrelazioni significative. Complessivamente, l’insieme di questi elementi indica un buon adattamento del modello, coerente con l’assunzione di residui gaussiani non autocorrelati.

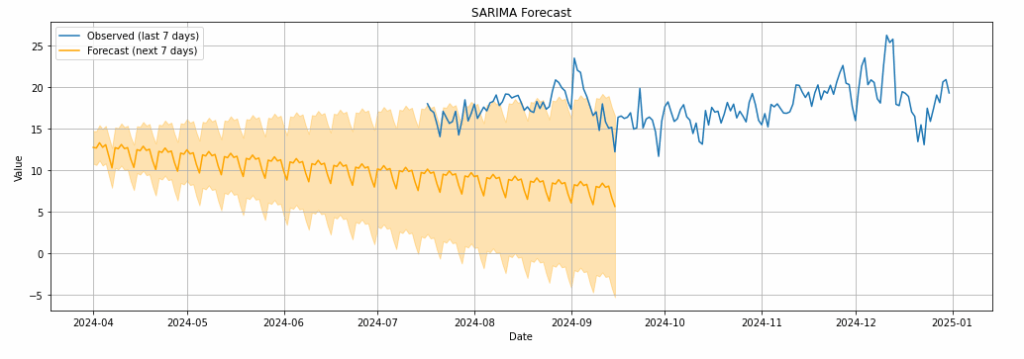
Interpretazione sintetica dell’output ottenuto

La figura mostra la previsione su un orizzonte di 7 giorni ottenuta a partire dal modello SARIMA stimato sulla serie aggregata giornaliera dei valori osservati della variabile oggetto dell’analisi.

La parte in blu rappresenta i dati osservati più recenti, mentre la curva arancione riporta la media della previsione condizionale per le sette giornate successive. Le bande arancioni sfumate rappresentano gli intervalli di confidenza al 95%, calcolati a partire dalla varianza degli errori previsivi.

Si nota immediatamente che il forecast manca di cogliere una componente rialzista macro (es. stagionalità a livello annuale, fenomeni esogeni che andrebbero catturati con opportuni regressori).
La stima della media risulta distorta verso il basso rispetto all’evoluzione reale.
La shape è eccessivamente semplicistica, questo dovuto anche alle semplificazioni apportate in sede di aggregazione dei valori per il run del modello su base giornaliera.
Gli intervalli di confidenza compensano questo errore solo in termini probabilistici, ma non aggiustano il centro della previsione e non aiutano ad ottenere una shape più realistica.
Il forecast riflette una stagionalità settimanale artificiosamente regolare, tipica di un SARIMA in assenza di altri effetti.

Tuttavia per le finalità esposte permette di portare a termine alcuni ragionamenti non necessariamente ovvi sui fattori che modellano l’andamento della serie storica.

Diversi effetti critici sopraccitati possono essere risolti o attenuati con un run del modello su un orizzonte più esteso e rispettando l’effettiva granularità oraria della time series.

Analisi econometrica e statistica di una time series con Python – Conclusioni

L’analisi condotta sulla serie storica oraria per un intero anno solare ha evidenziato la rilevanza dell’approccio quantitativo, sia in termini esplorativi che previsivi, nell’ambito dall’analisi delle serie storiche (time series).

L’impiego di tecniche statistiche classiche, integrate con strumenti di modellazione econometrica stagionale, ha permesso di ottenere una rappresentazione sintetica ma informativamente densa dell’andamento dei valori degni di osservazione.

In fase descrittiva, è emersa con chiarezza la struttura ciclica della variabile, con variazioni sistematiche tra ore del giorno e giorni della settimana, nonché la presenza di episodi anomali legati a fattori esogeni. La visualizzazione tramite heatmap ha confermato tali pattern, offrendo una lettura intuitiva dell’evoluzione temporale dei valori orari in modo immediato.

Dal punto di vista modellistico, la scelta di un modello SARIMA, applicato su una versione aggregata e semplificata della serie, ha consentito di gestire efficacemente la componente stagionale settimanale e di fornire previsioni affidabili su orizzonti di breve periodo. La struttura del modello stimato ha mostrato una buona capacità di adattamento ai dati, come testimoniato dalla diagnostica dei residui e dai criteri informativi ottenuti (in particolare l’AIC).

L’approccio adottato, pur basato su una semplificazione della serie oraria originale, si è dimostrato efficace nel catturare le dinamiche fondamentali del processo di generazione dei valori. Tuttavia, restano aperti diversi ambiti di estensione e approfondimento.

Una possibile evoluzione dell’analisi prevede l’integrazione di variabili esogene, come fattori reali di domanda e offerta, la produzione, variabili fisiche (es. meteo, temperature, fenomeni imprevedibili) all’interno di un modello SARIMAX. SARIMAX (Seasonal AutoRegressive Integrated Moving Average with eXogenous regressors) è un’estensione del modello ARIMA e del modello SARIMA, che consente di modellare serie storiche con componente stagionale e con regressori esogeni.

Un’ulteriore linea di sviluppo riguarda l’utilizzo di tecniche di machine learning per la previsione non lineare, oppure l’applicazione di modelli a frequenza mista o multivariata, in grado di catturare interazioni complesse tra più serie temporali.

Vuoi saperne di più o aver aiuto per le tue analisi su serie storiche?

Se vuoi supporto per i tuoi modelli, per la creazione delle tue pipeline di analisi dei dati, o per rafforzare le attività di Risk Management, contattaci!

Analisi econometrica e statistica di una serie storica con Python – scarica il Jupyter Notebook interattivo

In Aziona crediamo nel valore della condivisione della conoscenza! Scarica l’intero Jupyter Notebook interattivo sull’analisi di una serie storica al seguente link:

https://github.com/carloocchiena/code_bites/blob/master/python/time_series_econometrics.ipynb

Fanne buon uso e se ti è stato utile lascia una stella sul nostro repository!

Analisi econometrica e statistica di una serie storica con Python

Utilizziamo strumenti di analisi statistica e econometrica per l’analisi di una serie storica

Aiutiamoci con Python per la parte di analisi dei dati e previsioni di una ipotetica time series